This is the second of four essays in a series. The previous one, titled Boundaries Are in the Eye of the Beholder was about the property of reality of being “stable” enough to talk about it: all logic seems to point away from that possibility. In this one, I turn to the only line of reasoning that I believe resolves the paradox. The next one will build on this to assign the concept of “purpose” to its proper, non-confusing place.
- Boundaries Are in the Eye of the Beholder
- This essay
- Purpose from First Principles
- Carving Nature at Your Joints
Tennyson said that if we could understand a single flower we would know who we are and what the world is.
— Jorge Luis Borges, The Zahir
What is the source of what we call order? Why do many things look too complex, too perfectly organized to arise unintentionally from chaos? How can something as special as a star or a flower even happen? And, for that matter, why do some natural phenomena seem designed for a purpose?
We live in a universe of forces eternally straining to crush things together or tear them apart. There is no physical law for “forming shapes”, no law for being separated from other things, no law for staying still.
Boundaries are in the eye of the beholder, not in the world out there. Out there is only tumult, clashing, and shuffling of everything with everything else.
And yet, our familiar world is filled with things stable and consistent enough for us to give them names—and to live our whole lives with.
In this essay we’ll tackle these questions at the very root. We need good questions to get good answers, so we’ll begin by clarifying the problem. It has to do with probabilities—we’ll see why those natural objects seem so utterly unlikely to happen by chance, and we’ll find the fundamental process that solves the dilemma.
This will take us most of the way, but we’ll have one final obstacle to overcome, a cognitive Last Boss: living things still feel a little magical in some way, imbued with a mysterious substance called “purpose” that feels qualitatively different from how inanimate things work. This kind of confusion runs very deep in our culture. To remove it, I’ll give a name to something that, as far as I know, hasn’t been named before: phenomena that I’ll be calling—enigmatically, for now—“Water Lilies”.
Armed with this new tool for the mind, we’ll be ready to move on to future essays about the workings of the Universe with extra lucidity. So here we go.
Toy Examples of Things Not Likely
Let’s begin by assuming that no “cosmic purpose” or divine intention is at work, magically directing the transformations of the Universe. Also, suppose there isn’t any invisible “world of the spirit” or “mind” that affects our material world in mysterious, non-physical ways. (We’re going with Pierre-Simone Laplace here: there is no need of those hypotheses.)
What do we have that we can work with, then? One fundamental rule we have is the Law of Conservation of Energy: energy is transformed and transferred during interactions, never destroyed. But that is not enough on its own. A single interaction like a particle decaying into two other particles, say, can be described precisely in terms of energy, with a range of physically allowed outcomes, but it doesn’t need to lead to any specific outcome in that range—much less contribute to more complex outcomes like a crystal, a volcano, or a kangaroo.
To be clear, a single physical interaction doesn’t exclude the (eventual) production of kangaroos or diamonds. Those outcomes are physically possible, but you would need a very long, very specific sequence of interactions in order to produce those things. You need the elementary particles to somehow assemble, one after the other, in enormous numbers, each in a fairly specific position, like the steps of an Ikea instructions manual.
That sequence of events is what instinctively feels too unlikely to happen.

Since each interaction is random and has several possible outcomes, assembling larger objects is a bit like rolling a sequence of dice. If you represent a physical interaction with a 🎲 die roll, then getting to a complex, stable outcome like (say) a flower would be more difficult than rolling enough dice to fill a container ship—and somehow getting only sixes.
If you’re a little familiar with the probabilities of dice, then you know that the number of possibilities gets astronomical really fast.
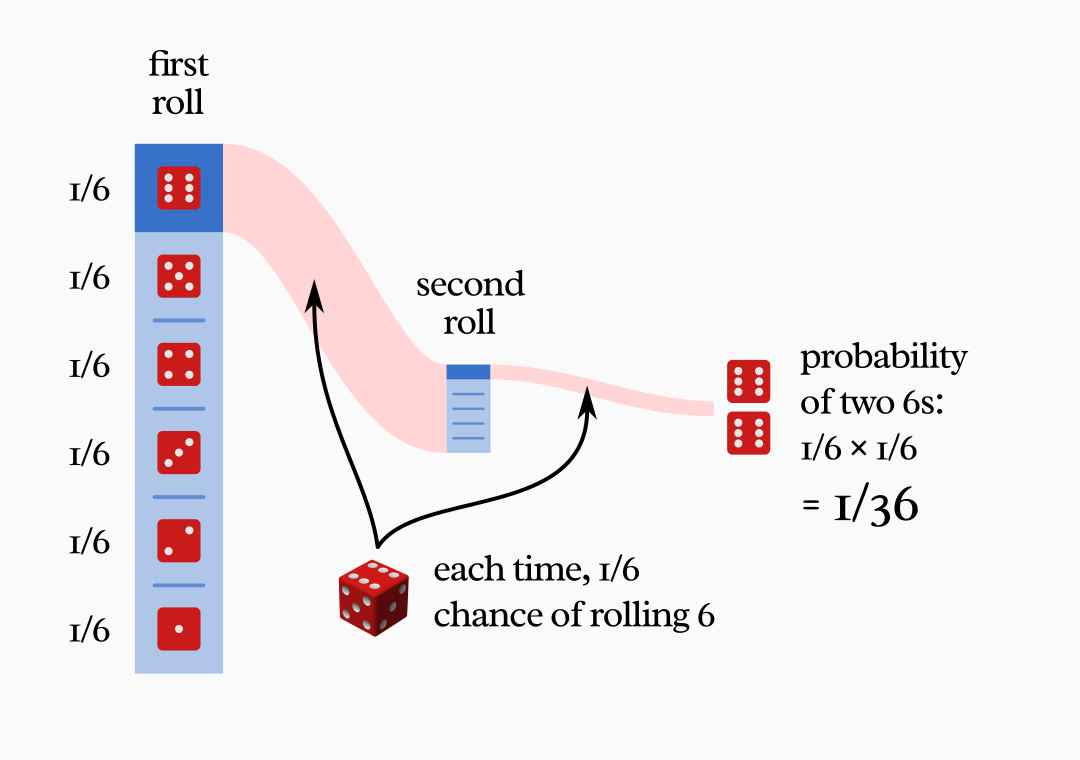
Getting two sixes in a row has a 1 in 36 chance.
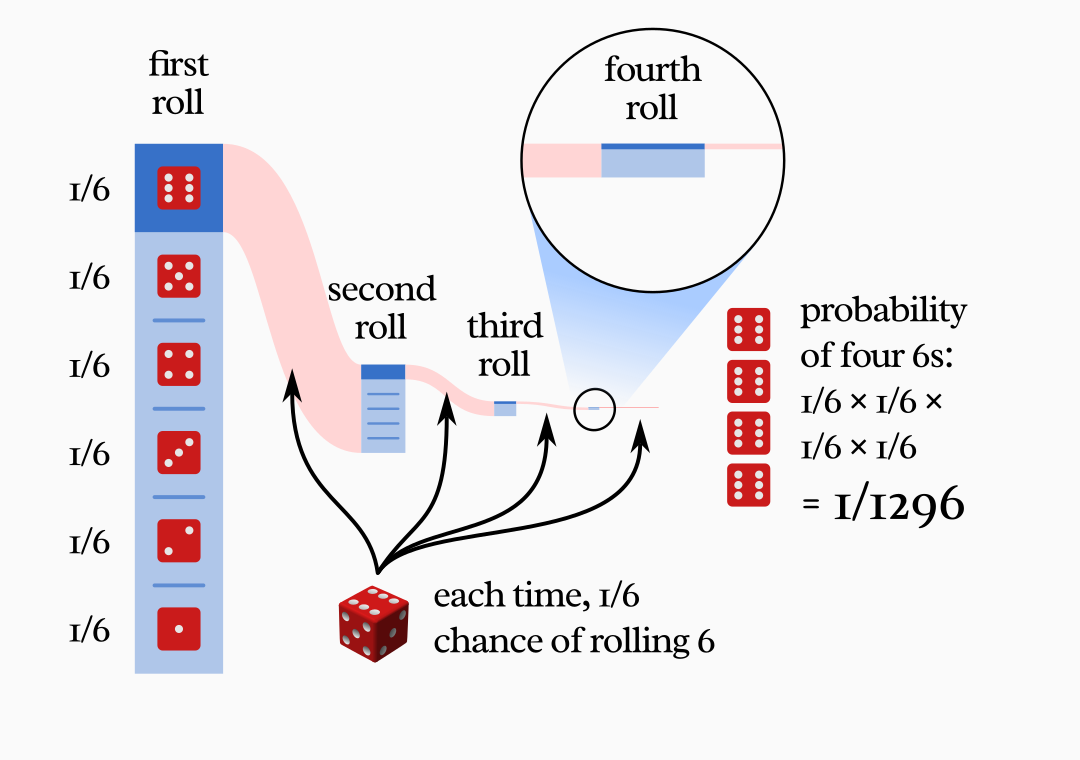
The probability of four sixes in a row is 1 in 1296. Beyond that, you can’t even draw a meaningful diagram to scale, because the lines would get way too thin. Ten sixes in a row would have a probability of , and in the case of forty it would be
(We would need many more digits for the case of the dice-filled cargo ship, but I’ll spare you those pixels.)
This dice-rolling analogy is easy enough to grasp, and it clarifies what we mean by the probability of sequences of events. But, it turns out, it vastly underestimates just how improbable things get in the real world.
Besides, dice are a rather weak metaphor of how things interact in the future because, by definition, each roll is independent from the previous ones and subject to the same circumstances. Real-world interactions, on the other hand, usually build on top of each other leading, at each event, to novel possibilities every time.
Lego bricks, which can be assembled indefinitely, are a much better representation. Start with a single brick. For example, a three-stud brick like this:

Suppose you want to add a second three-stud brick on top of it. How many unique ways are there to attach it? I count eight:
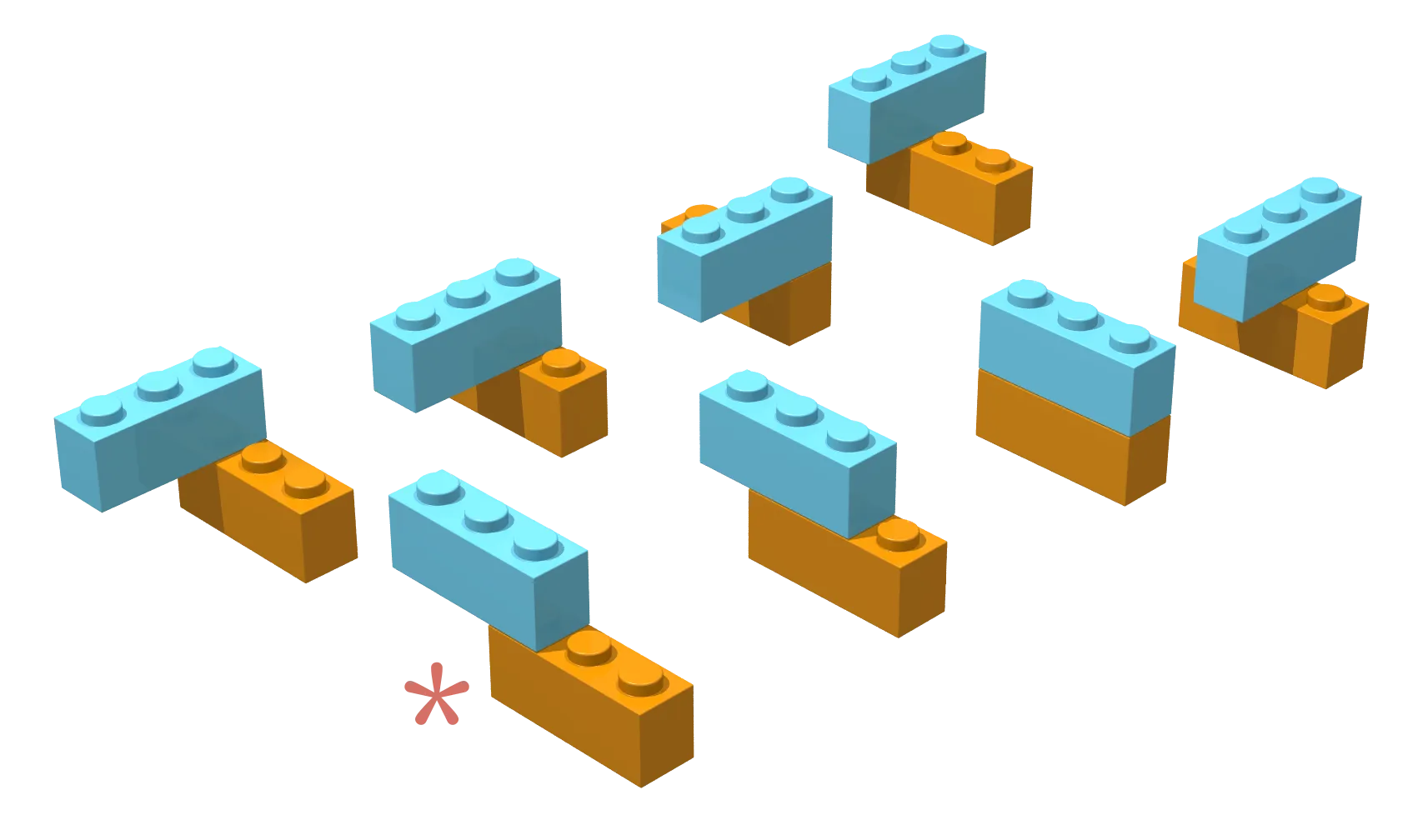
(Here we can ignore the colors, so I’m not counting the arrangements where the green brick goes under the yellow one, because they would be equivalent in shape to those shown in the image above.)
Imagine we have a way to randomly assemble the bricks, like a brick cannon shooting blindly (we’ll see a more realistic method later). Each of these eight shapes will have some probability of happening. Some of these structures are more likely to happen than others, because of their symmetrical properties, but let’s not worry about that here. At first approximation, these combinations have a probability of about 1/8 (12.5%) of happening by chance.
What if we want to add a third brick of the same shape to the assembly? This becomes considerably more complex and time-consuming.
Instead of looking for all combinations, I will focus only on the combinations that build on the two-brick structure with the asterisk next to it in the previous image. To preserve my sanity, I divided them into three groups: 1) when the third brick goes on top of the second, 2) when the third brick goes on top of the first, and 3) when the third brick goes under the second. This gives us 30 possible structures:
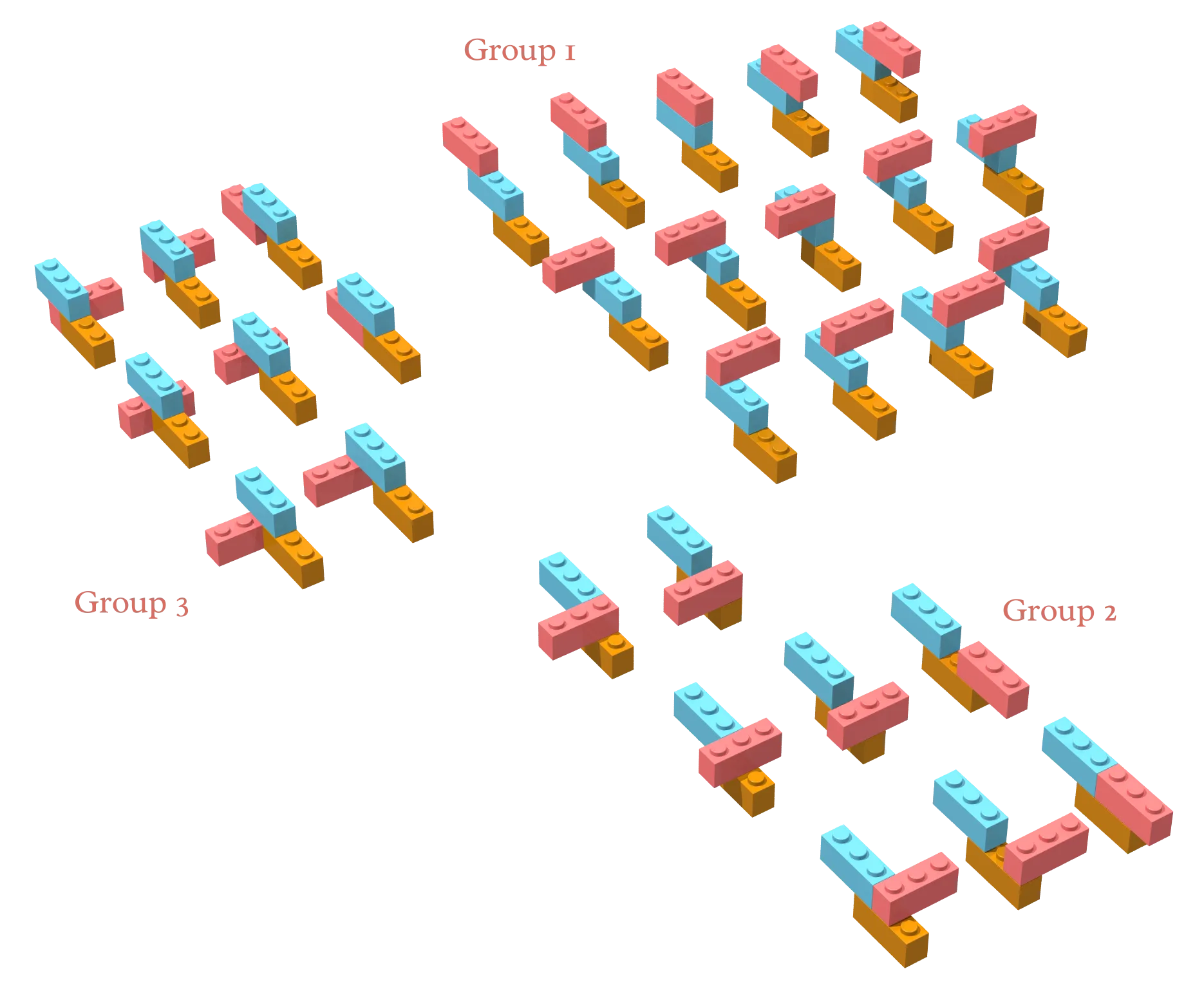
Since I based these results on only one of the initial eight two-brick assemblies, I would have to repeat the count all over again starting with each of the other seven base assemblies, remove any duplicates, and come up with a full list.
Already, with only three puny bricks, I’m exhausted. It’s hard to give a precise number without doing it all manually (or writing an advanced algorithm that computes it for me). I would estimate that there are more than 100 unique ways to put three three-stud bricks together. Given a random process, this means that some configurations have less than a 1% probability of coming up at random.
Imagine adding one more brick. For each of those 100+ three-brick configurations, we’d have dozens of ways to add the fourth brick: on top of the third or under it, on top of the second or under it, on top of the first.
Or imagine doing the same survey with two-by-four bricks instead—with eight studs each instead of just three. Now two bricks can go together in 24 distinct ways (compare it with the eight ways for the three-stud case), and three bricks give 1560 combinations! The numbers become unmanageable much faster.
Søren Eilers, a mathematician at the University of Copenhagen, has gone much further than me with the calculation. He studied two-by-four brick combinations with a proper algorithm, with the following results.
| # of bricks | 2 stories high | 3 stories high | 4 stories high | 5 stories high | 6 stories high |
|---|---|---|---|---|---|
| 2 | 24 | ||||
| 3 | 500 | 1,060 | |||
| 4 | 11,707 | 59,201 | 48,672 | ||
| 5 | 248,688 | 3,203,175 | 4,425,804 | 2,238,736 | |
| 6 | 7,946,227 | 162,216,127 | 359,949,655 | 282,010,252 | 102,981,504 |
For the six-brick case, the total number of unique structures is 915,103,765 (the total sum of the last row in the table). That’s almost a billion ways, and it took Eiler’s computer several days of number-crunching to reach.
Now that you have a better sense of the numbers we’re talking about, take a look at this array of about a thousand pieces of various shapes and sizes:

There isn’t a supercomputer on Earth today that can spit out the number of possible arrangements of those pieces in less than many times the Universe’s lifetime. The probability of randomly getting this specific arrangement of those same pieces:

…out of all the possible arrangements is so vanishingly small that we can’t even hope to compute it.
Lego bricks are a great example of something that happens constantly in nature: atoms, molecules, genes, people, companies, and so on interact, build on each other, and lead to new things without end, and in much greater numbers and variety than the toy examples above.
Some improbable processes are less Lego-like, though. Lego works by addition, but other things work as sequences. If you tried to reach the Great Pyramid of Giza from your house by walking randomly, you’d be very unlikely to get there: there are many sequences of steps that will take you there, but many more that won’t. The same for a tree leaf converting the energy of a sunbeam into chemical energy, or a chef preparing a delicious croquembouche pastry.

In all these long sequences of interactions and transformations, the process—be it a human trying to achieve something or a mindless process unfolding naturally—is made up of many small steps, each of which is required to land in a small subset out of many possible outcomes. Like rolling dice in sequence.
Here we’ve come to the heart of the paradox. If you focus on any single interaction, driven by mindless forces, it’s impossible to explain how it would lead to one specific, interesting outcome, instead of many others—and do that again and again. For example, given that every water molecule is attracted by other molecules at random, why would trillions of them arrange themselves into pretty snowflake shapes just so, with straight lines and regular angles?

Back to the Basics
There is, of course, a way out of this conundrum. By now, one thing is becoming clear: if you look at one interaction at a time, like a pair of bricks connecting to each other, nothing but undifferentiated randomness seems possible. If all there was to physics was a series of isolated events, destructive chance would reign supreme. The key, then, must be to look at chains of interactions, instead of single ones. This is how things begin to get exciting.
When you have multiple connected interactions, you can get two kinds of outcomes—one straightforward and the other much more interesting.
Type 1: Open Chains
The straightforward kind is an open chain of cause and effect like this:
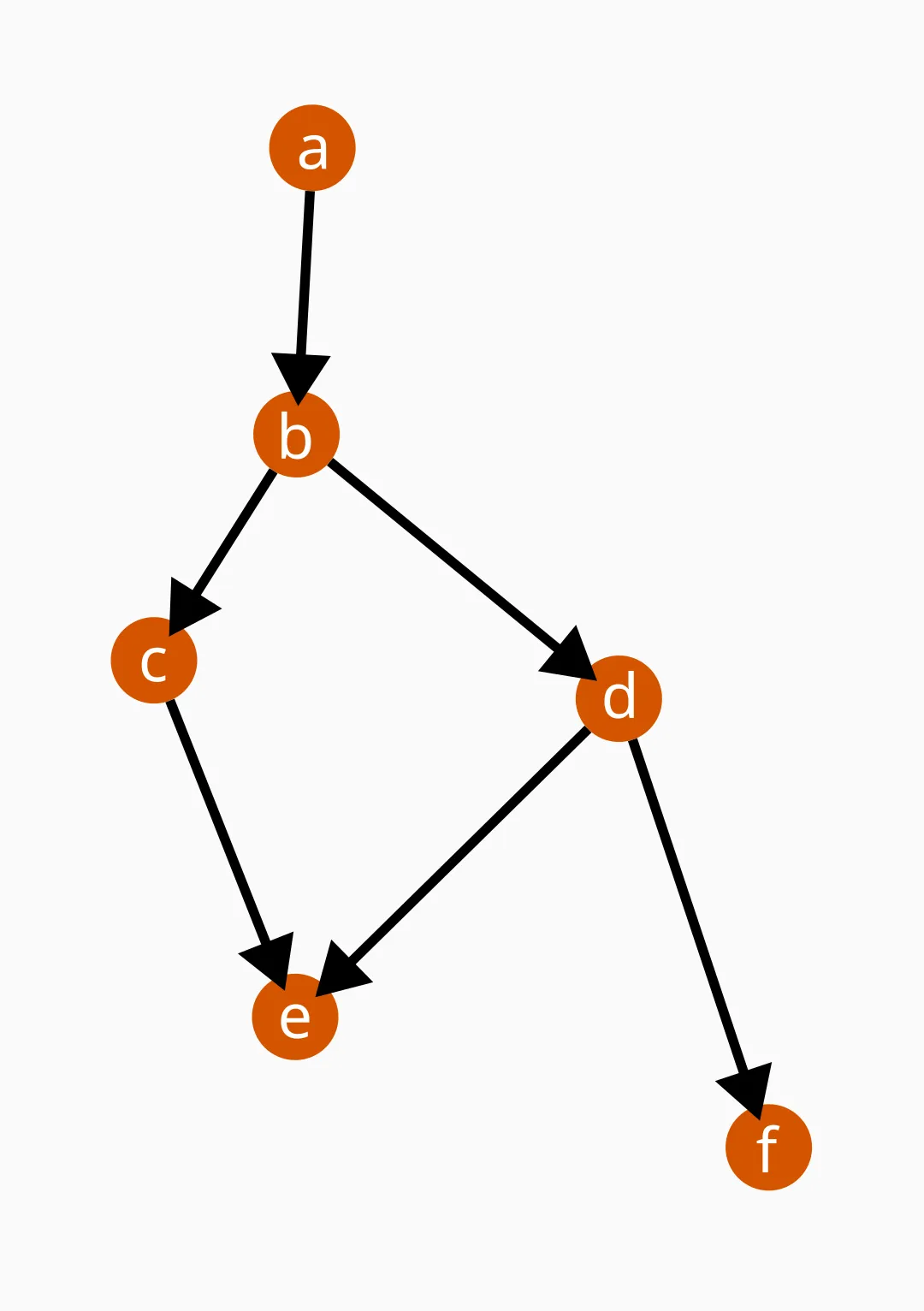
It’s a cascade similar to an avalanche or a domino-toppling performance. This is equivalent to the dice-rolling sequence example and to the cannon-based random assembly of Lego bricks. Chaos still reigns supreme here, and there is no escaping it. No specific result is especially favored.
Type 2: Loops
The second kind of outcome you might get with multiple interactions is something like this:
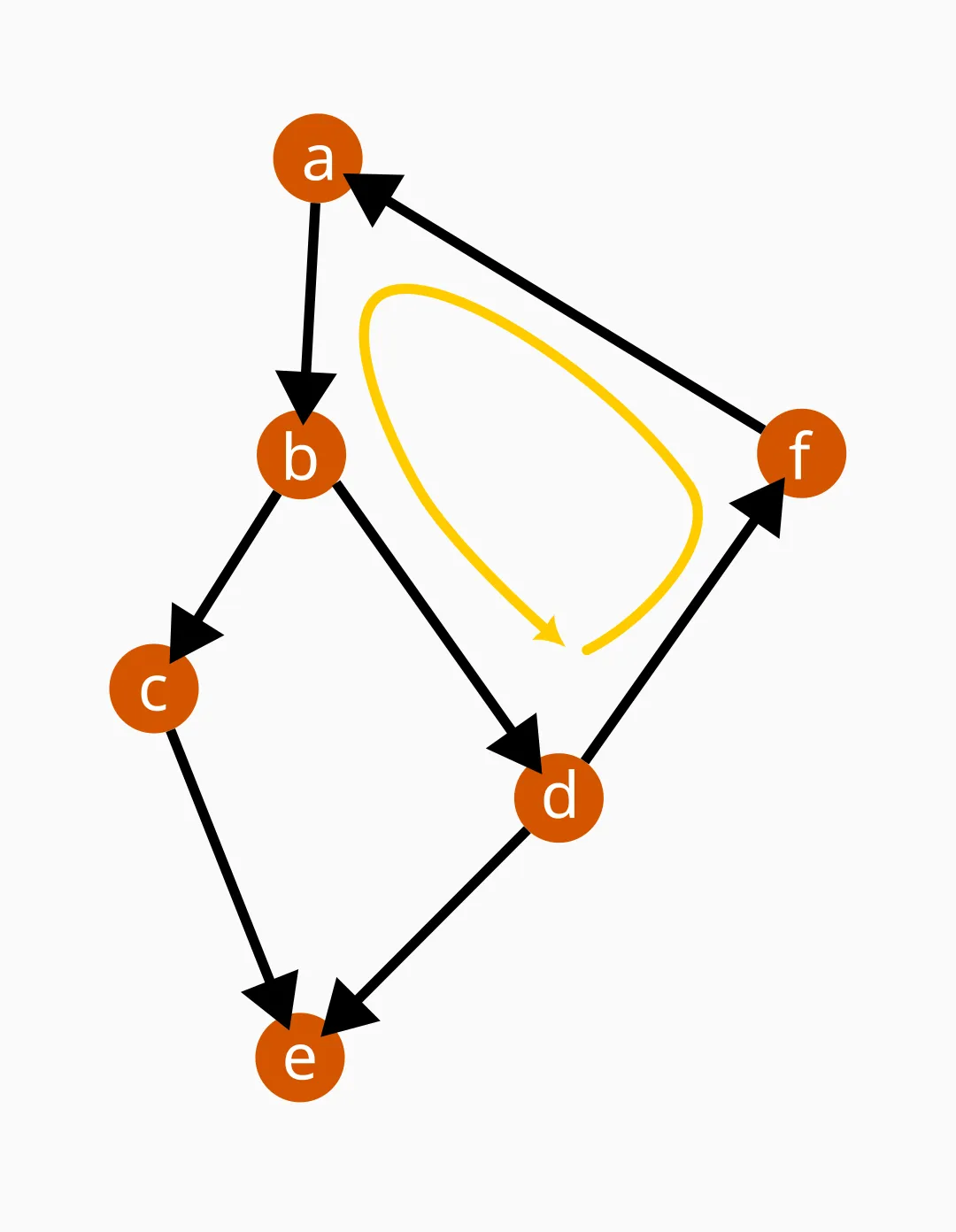
In this case, later interactions feed their outcomes back to affect the objects and processes that caused them in the first place. The cause-and-effect chain “loops back” into itself.
We can call this phenomenon feedback. The difference between the linear chain of events and the self-affecting closed loop above is a case of emergence, a change from zero to one, so to speak.
This closing of loops has profoundly transformative effects. I associate it (with a bit of poetic liberty) with what happens when you align two mirrors in front of each other: before, they were merely reflecting the world around them; the moment they face each other, they spawn this terrifying dark universe of infinite recursion.
Feedback makes recursion possible, and recursion is what makes the unlikely likely.
To see how that is possible, let’s return first to the dice-rolling example. Suppose you roll a die several times, but now every time you get a six, for the next roll you’re allowed to pick a new die that is a bit more “loaded”—a bit more likely to result in a six. You begin with a fair die, with every face equally likely, but getting a six makes it more likely to get a six again the next time.
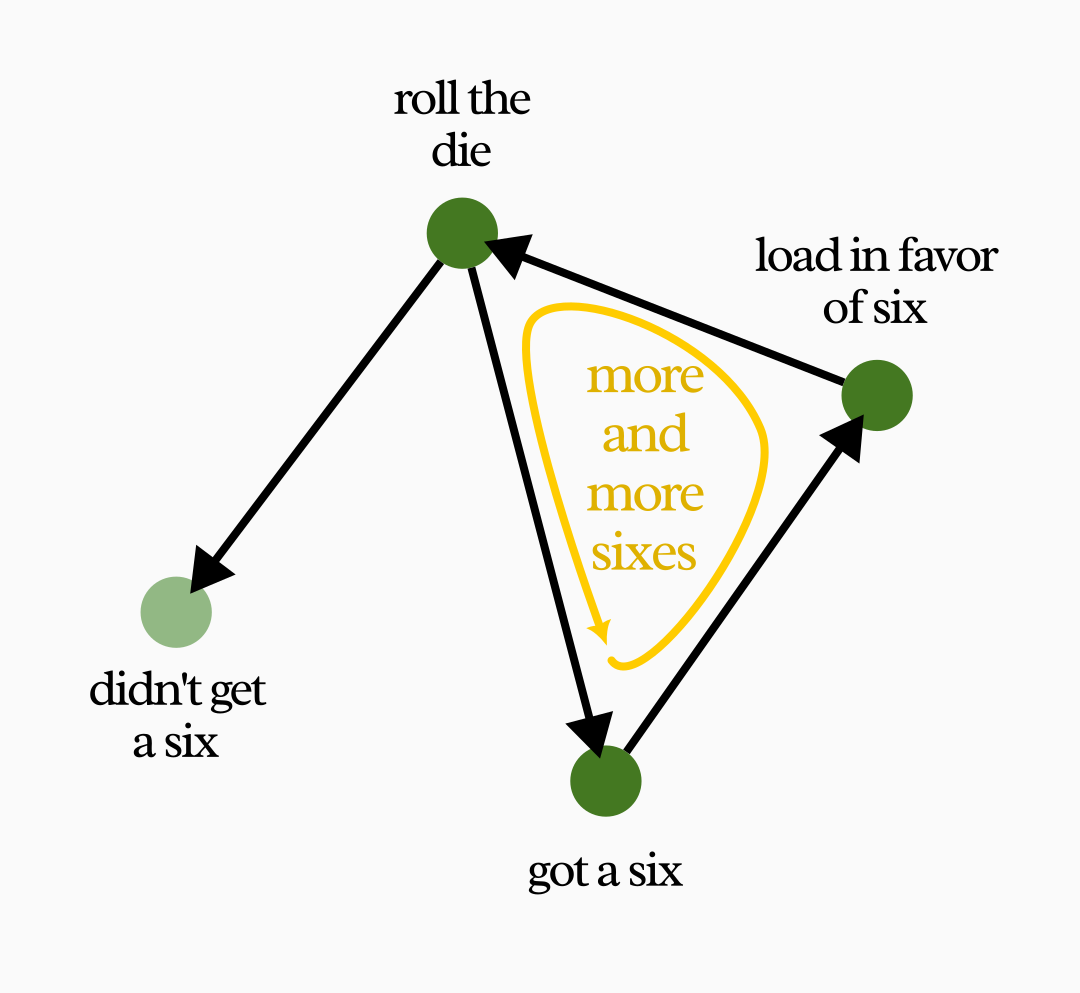
On the first roll getting a six is just as likely as getting any other number. Even if you do get a six the first time, the loading rule doesn’t guarantee you’ll get another one on the second roll. But things get more interesting as you roll more sixes.
Supposing each die is loaded so that not getting a six is 50% less likely than the previous die, you’ll get a sequence like this:
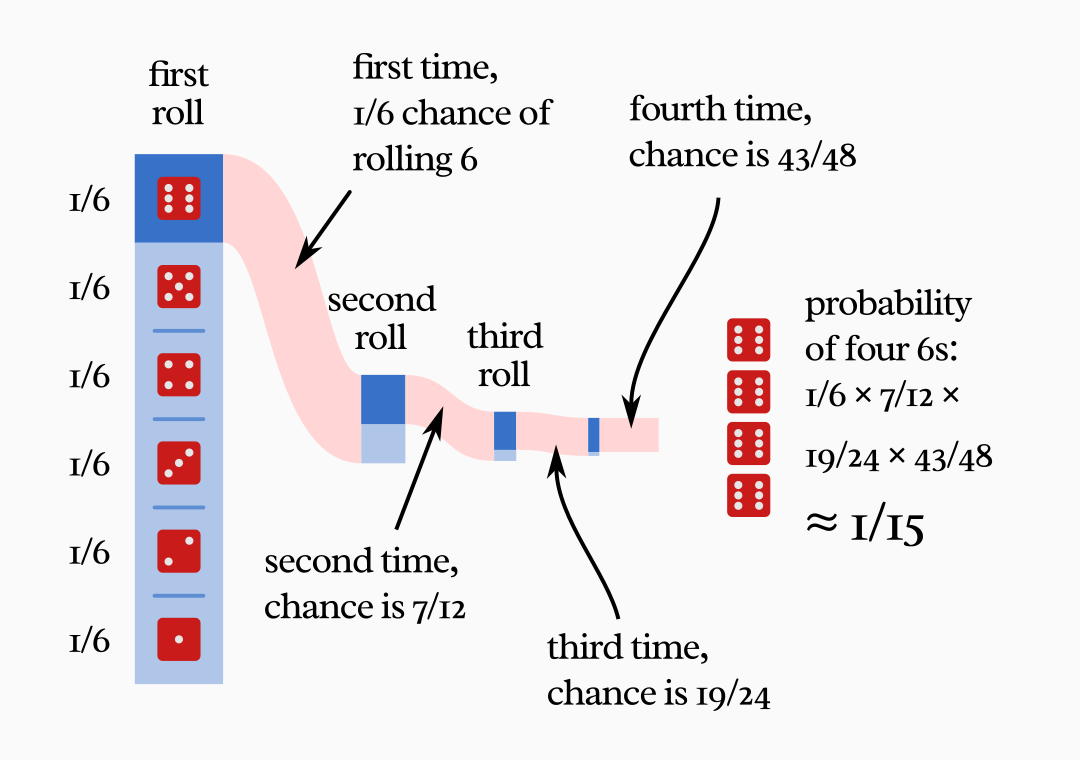
In other words, getting a six skews the Tree of Possibilities of future dice in favor of more sixes.
The probability of getting four sixes out of four rolls is now roughly 1/15. Compared to the 1/1296 of getting four sixes with fair dice, it is more than 86 times more likely. What’s more interesting, by the time you’ve gotten those four sixes, the dice you roll are so loaded that you’re almost guaranteed to keep on getting more sixes after that. The chance of getting ten in a row is 1/16, and that probability doesn’t significantly decrease if you want forty sixes out of forty rolls: it’s still roughly 1/16, one million trillion trillion times more likely than getting that same result with fair dice.
Although 1/16 may still sound rather improbable, it’s a huge improvement. This is especially true if you consider that, in nature, many random interactions can happen in parallel—for instance, particles bouncing around in a gas.
Imagine having a classroom of 30 kids playing this game of 40 die-rolls just once each. In the non-loaded case, the chance of even one kid getting 40 sixes straight is still so low as to be basically zero. With the feedback that gradually loads the dice, the chance is now 86%. The feedback mechanism we invented made something almost impossible into something more likely than not, even in the presence of randomness.
Of course, this artificial example works because we imagined manually picking ever-more-loaded dice based on the result of our rolls. Without a human doing that rather tedious work, rolling many sixes in a row remains very improbable. It’s not a naturally occurring process. But this example demonstrates that, assuming there is some process that influences the probabilities of its own future outcomes, things that used to be improbable can happen quite easily.
Again, things get more realistic if we use toy bricks instead of dice. What could be a less-contrived feedback process involving Lego bricks?
More than Clean Bricks
As with everything related to Lego, someone tried this already. (Equally unsurprising, it’s another mathematician.)
The man, a professor at the University of Jena in Germany, is called Ingo Althöfer, and his contribution to the field of Lego science was pouring a bucketful of them into a washing machine and pressing “Start”.

Now, the report he published wasn’t peer reviewed, it’s not written as a serious paper, and it’s admittedly rather tongue-in-cheek. By no means is it useless or poorly executed, though. What Althöfer found is that many pieces stick together during washing, forming structures of two, three, or more pieces by the end of the cycle. For instance, after washing 326 separate two-by-four bricks in the machine for over an hour, this is what he found:

Out of the washer came 72 structures made of two bricks, 13 made of three bricks, and gradually fewer for larger structures. Around 130 bricks, or 40% of the original number, remained separated.
This is strange, because it’s hard to imagine a more random process than tumbling in violent water. Why aren’t there more shapes? What happened to all the other billions of combinations counted by Eilers? Althöfer repeated this experiment hundreds of times, always with similar results. Why did he always get roughly the same proportions between those few outcomes?
A follow-up experiment by Althöfer sheds some light on this question. He tried putting pre-formed pairs into the washing machine. Before the washing, they looked like this:

The numbers on the bricks indicate how many pairs of that color he used. Notice how these pre-washing pairs are monochromatic, with no mixing of brick colors. After the washing, the professor found this:

And this bucket of loose bricks:

From this, you can notice a few things:
- Many of the original two-brick structures remained unchanged (left half side of the second-from-last picture).
- Some of the original two-brick structures have grown with the addition of one or more bricks (middle-right group in the second-from-last picture).
- Many of the original structures have been broken down into single pieces (the bucket picture).
- Some of the broken-down pairs must have recombined into new two- or three-brick structures, because many multicolored structures came out of the machine (right-most group in the second-from-last picture), whereas they were all monochromatic before washing.
In other words, there are two processes happening at the same time: breaking down and building up.
But, again, not every imaginable outcome is coming out of the washing machine. None of the resulting structures have bricks attached by fewer than six studs to each other, for example. Also, none are joined at a 90-degree angle, and none have more than five bricks together.
The reason for this bias in outcomes is the different stability of the various combinations. It’s not that those billion missing shapes aren’t forming at all during the random collisions: they do form, but the vast majority are unstable and break down at the slightest bump.
Even assuming that each collision between two bricks is random and has no preference for the structures it will form, most of the resulting structures will break down immediately and thus won’t come out at the end.
Smaller structures are more numerous than larger ones because, again, the larger ones break down more easily. But they are more common also because two smaller structures need to form first before they can combine into a larger one.
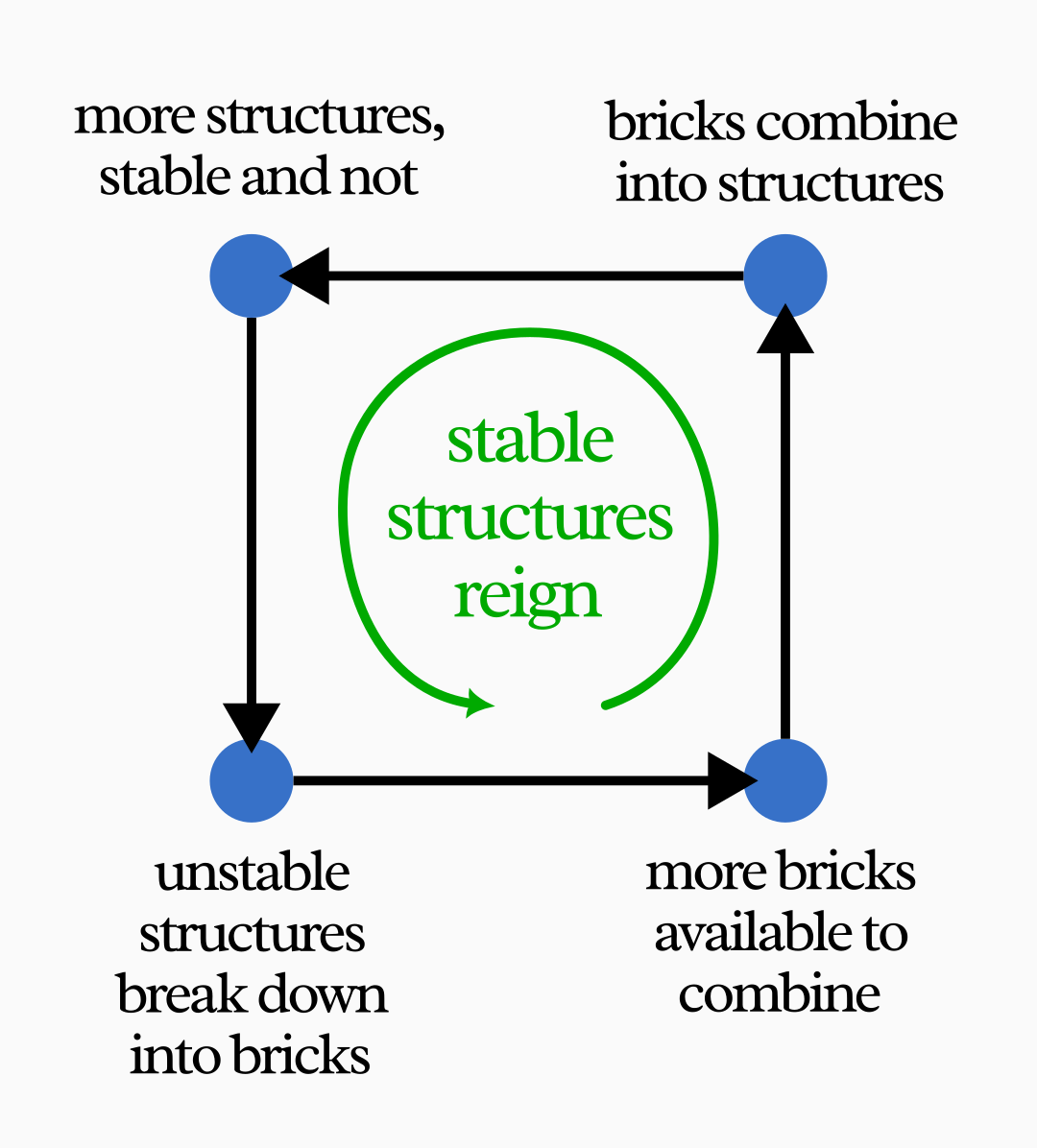
If there are too many loose bricks in the washing machine, forming two- or three-brick structures is easier, because there are more collisions between single bricks. If there are too many big structures, their rate of breaking down will surpass the rate of growth. These are balancing processes that favor certain mid-way outcomes over all the other possible ones.
This is a great example of a kind of feedback that happens often in nature. If you replace the bricks with bits of DNA molecules, “stability” with “fitness”, and “bumping into each other” with “recombining and mutating”… you see where this is going.
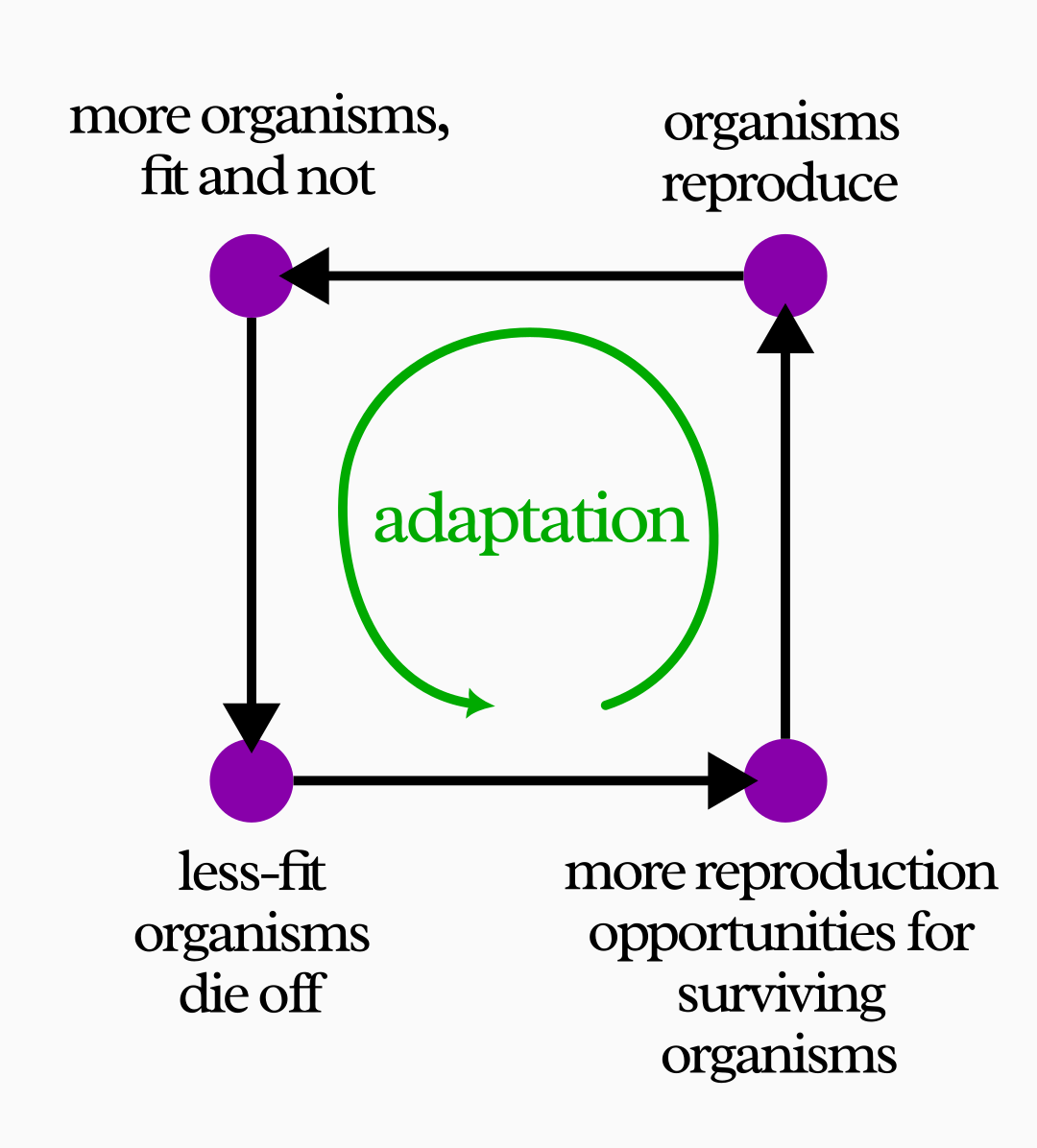
This “washing machine + loose bricks” system is able to produce, over and over, the same predictable distribution of a few structures, out of the gazillion possibilities that Eilers has shown to be theoretically possible. And it can only do it thanks to a feedback mechanism.
Some Things Are Under Control
We come now to the part that gives rise to enormous amounts of confusion in science and in life in general.
The most well-known and understood kind of feedback is what scientists and engineers call “control”. This is what’s going on when you’re trying to thread a needle: you apply a very tight feedback loop. First your eyes see the relative positions of thread and needle-hole, and determine the direction your hand should move to close that gap. Then you try to close the gap a little. Then you see the new relative positions, and so on until the thread is through.
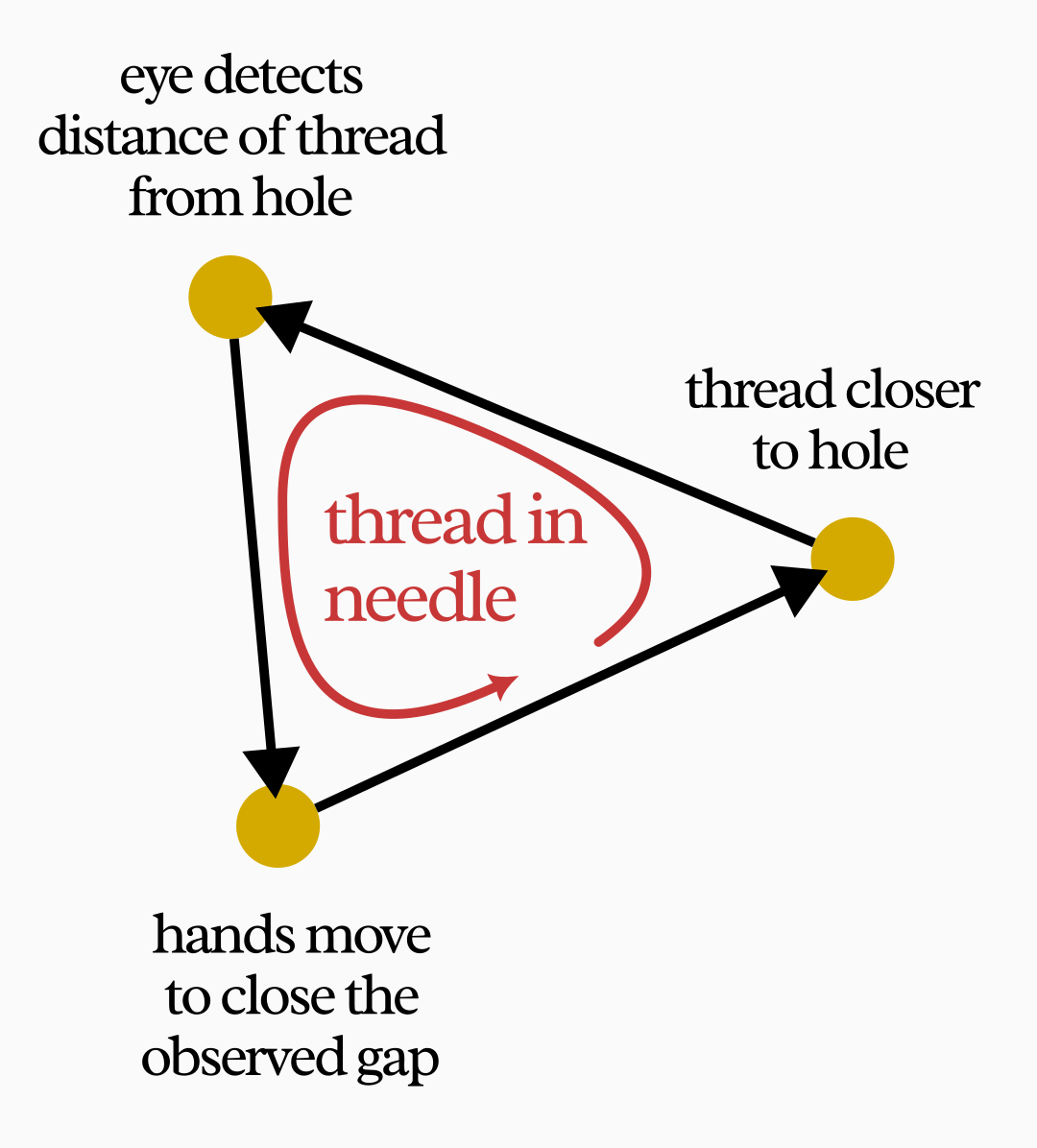
Of course this is a case of feedback, because each movement and observation goes to affect the next movement and observation. Threading a needle with random jerks of your hands, with your eyes closed, is very unlikely to work, but the repeated control cycle of eye and hand makes (with some training) that same outcome likely.
Control is also what you would use to build the improbable Lego house we saw before. For each piece you add, you use your sight and touch to sense the discrepancies from the configuration shown in the instruction sheet, and your muscles to “correct” those discrepancies. Do this long enough, and you’re almost guaranteed to arrive at the desired shape, no matter how many trillions of other shapes are possible.
Inventors and engineers were the first to clarify the concept of feedback and control loops, because it’s the only way to systematically design mechanisms capable of reaching and maintaining specific states in the face of random external forces.
The classic example is the thermostat, a simple mechanism that measures a room’s temperature and, if it is lower than a predefined value, automatically turns on the heater. Conversely, when the temperature goes above the desired level, the thermostat turns the heater off. In this way, the room remains more or less at a constant temperature: something improbable in the absence of feedback.
A modern car—to take just one example among many that surround us every day—is crammed full of feedback systems in order to stay within its ideal ranges of operation. There is a control loop in the engine to balance the amount of air and fuel, adding more of one or the other when the proportion would lead to inefficient performance; another loop controls the engine’s rhythm while idle, to keep it steady and fuel-efficient; cruise control is another feedback loop, stabilizing the car’s speed; and more loops are in place to maintain the optimal wheel rotation speed, the amount of damping in the suspensions, the battery’s voltage, the cabin’s air temperature, and so on.
Don’t even get me started talking about the sheer, mind-boggling amount and sophistication of the control mechanisms in something like a rocket or an airplane. Those things couldn’t fly further than a stone-throw without a thousand feedback loops to keep them stable.
In each of these systems—the thread-eye-hand loop, the thermostat, the car’s speed control—someone picks a specific “goal state”, and then a mechanism to eliminate the differences between the current state and that ideal state.
In other words, this engineering view of feedback gives us a clear link between the definitions of “goal” and “control”:
Definition 1
A goal is a particular system state that a human wants to achieve by avoiding all different states;
→ the process used to achieve a goal necessarily involves feedback, and we call it a control mechanism.
This is where the confusion arises. Since the idea of feedback began in engineering, many still associate it with human-made things. It is very natural, in this context, to expect the definition above to be applicable to all feedback systems, not only human-designed feedback systems. It feels universally acceptable to say that the goal comes first, and the feedback later.
But this reasoning is backwards. As we’ll see below, nature is full of “unintentional” feedback loops—none of which have pre-defined goals.
When you walk, multiple feedback loops are at work. One is, of course, the control loop to get where you want to go—reducing the distance between your current location and a goal location you have in mind. But you also have feedback loops that you’re not even conscious of. Just to remain standing or sitting, your body is constantly perceiving your current posture and applying small corrections with muscles all over your body. At any given moment, you breathe faster or slower based on how much oxygen your lungs need. The same goes for your heartbeat, your eyelid movements, and a million other things your body is doing while you think about something else. The complexity here far exceeds that of even the most advanced rockets.
Can we still say that these bodily functions have “goals”, like the machines we build? Although they are more organic and complex, they certainly follow the same principles of observation and “error-correction”, and in that sense one might argue that they are control mechanisms.
But there is a clear distinction to be made: the control mechanisms of a machine and your conscious body movements unfold after you’ve thought about its goal in your head, while in the unconscious physiological loops the goal seems to be “simultaneous”, embedded in the mechanism without preceding it. That goal wasn’t produced by any thinking process—it wasn’t the starting point.
This distinction, I believe, is key to a good understanding of anything in nature.
Mindless and Lifeless Feedback
It is the consistent behavior pattern over a long period of time that is the first hint of the existence of a feedback loop.
— Donella Meadows, Thinking in Systems: A Primer
I wrote above that it’s a stretch to describe a bodily function like breathing regulation as a feedback loop with the “goal” of keeping you alive. We can dial that question up a notch: what about plants?
In There Is No Script in the Life of a Water Lily, I mentioned some of the countless feedback mechanisms that make the blooming of a flower possible: mechanisms to make it grow reliably upwards, to make it stop growing when it has reached the surface, to make it open and close at the right times, and more. It’s possible, in theory, for a disordered bunch of atoms to “fall into place” together without feedback, pushed by random non-looping chains of events into just the right configuration to make a living water lily. But although this is physically possible, it’s even more unlikely than the Lego house we saw above. So unlikely that we can ignore the possibility.
Even if, somewhere in the vast Universe, a flower did happen to come together, fully formed, by mere happenstance—perhaps a lucky collision of particles in a supernova nebula—it wouldn’t last long in that form, and the likelihood of the same thing happening again would be no higher than before.

Yet, when the causal chains close and feedback happens like it does on Earth, the flowering of a water lily becomes a frequent, ordinary phenomenon. It happens many times, in every lily pond, every year, over and over! Here, like in the machines and the intentional actions of people, feedback enables the repeated, continued emergence of patterns of existence that would be too unlikely with the random sloshing and remixing of elements. But it’s hard to argue that the plant’s actions are goal-directed. They don’t even have nervous systems.
Biologists are careful not to attribute things to purpose too easily—evolution, after all, is mindless and uncontrolled. But you might still be led to believe that feedback arose as a prerogative of living things. Both the dice and the Lego examples I gave above seem to require a human to select them or throw them in washing machines. Is feedback, perhaps, the key marker of life?
Not at all. On the contrary, feedback is the basis of phenomena much more fundamental than life and machines.
The pebble that is rolled about by the movement of the sea tends to assume a smooth surface that will aid further rolling. The effect here is the movement of the pebble which retroacts [=feeds back] on the resistance to movement factor rendering it continually less resistant. The more the pebble rolls, the more it wears away its irregularities, so the better it rolls—an example of positive retroaction [=feedback]; the pebble tends towards the annulment of its resistance.
— Pierre de Latil, Thinking by Machine
The pebble isn’t smooth from the start. Its roundness is not due to a lucky accumulation of minerals just so that they end up in a smooth and simple shape. It’s the feedback loop the pebble is caught in that gives it that shape, and the same happens trillions of times more to other stones in the wide seas. A very improbable state—a sleek round stone—becomes likely through feedback.
Or take the innards of a massive star. Most of the time, stars are made of a mixture of elements of different atomic weights. These elements all interact with each other randomly, but they result in this:
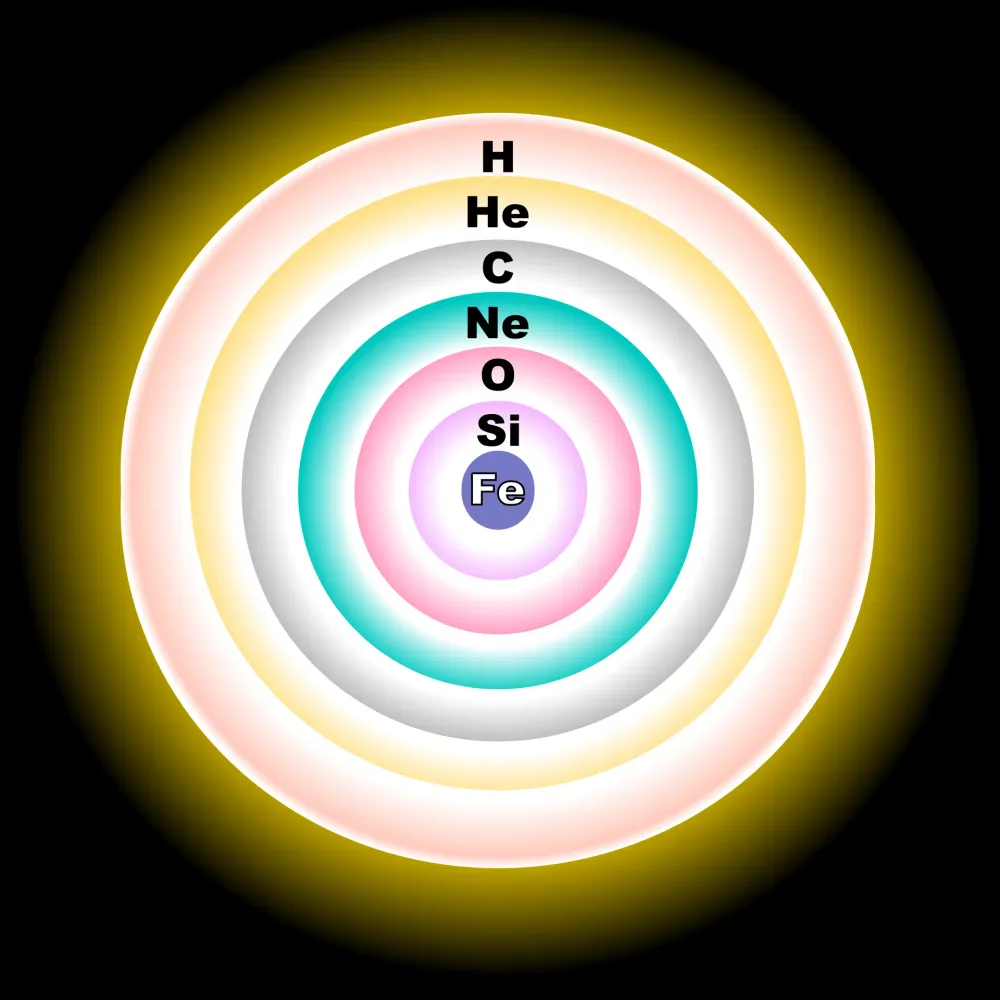
The heavier an element is, the closer it is to the center of the star. Silicon (Si) nuclei are lighter than Iron (Fe) nuclei, and they “happen” to be in a shell above; oxygen (O) is lighter than silicon, and it sits above it; and so on in tidy concentric shells all the way to the surface, which is made of hydrogen (H), the lightest element.
That’s a very non-random way for the star to arrange itself. Haphazard mixing of materials doesn’t look at all likely to produce this kind of tidy stratification.
Had we somehow observed the insides of a star in pre-scientific times, we might have been compelled to attribute this neat layering to the inscrutable goals of an obsessive god. But today we know that the stratification happens, not in one but in trillions of stars around the Universe, because of other—admittedly, sneakier—feedback loops.
A first-generation star begins as a hydrogen ball, where gravity-induced pressure triggers a repeating cycle: as nuclear fusion in the core converts lighter elements to heavier ones, the released energy temporarily counteracts gravity’s squeeze; when that fuel depletes, energy emission weakens and gravity compresses the star further, raising temperatures enough to fuse the next heavier elements. This process recurs many times, resulting in an onion-like structure of concentric spherical layers, with the heaviest elements at the center and progressively lighter ones toward the surface.
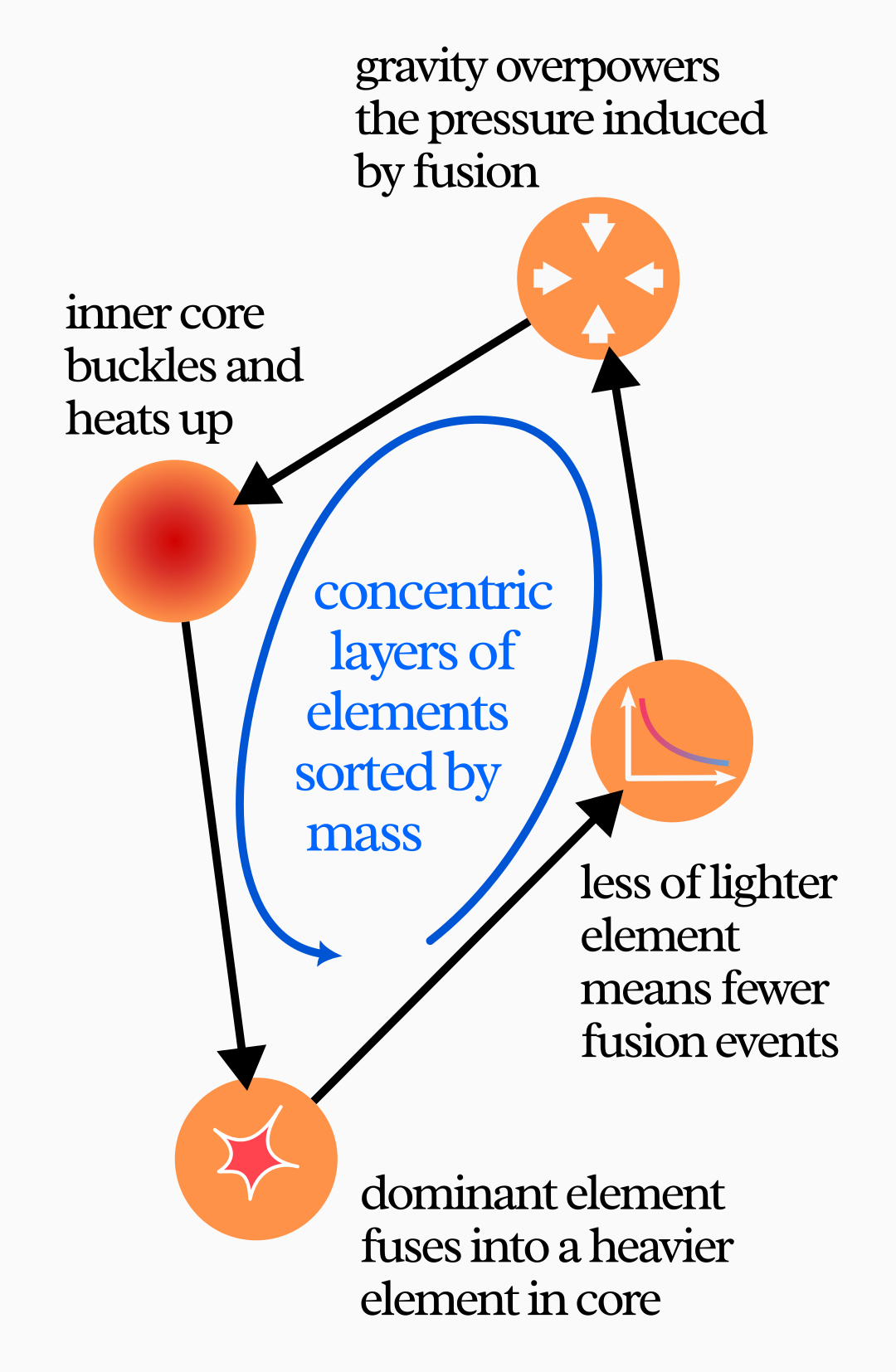
This process is aided by buoyancy, which makes less dense plasma float above those that are denser—another feedback loop, although I’ll leave the explanation of its mechanism to you as an exercise, if you’re curious.
You can find any number of other non-living examples of recursion out there: the spherical shape of stars and planets, any kind of elasticity, the “solidity” of solid objects, the existence of rivers and ocean currents, chemical reactions, the capture of electrons around atomic nuclei. While feedback alone is too general to fully explain the particular outcomes of all these processes, it is a necessary driver for them.
None of these phenomena have anything to do with life, intention, or goals. They are like the water lily—an almost impossible outcome made probable by feedback—but we would be wrong to describe them as goal-seeking or error-correcting. There is no design: they just happen because their interactions affect themselves recursively.
Water Lilies, Capitalized
Going back to Definition 1 above, notice that “goal” and “control mechanism” come as a pair. The two concepts coexist like two sides of the same coin. You can’t have a goal if you don’t have a control process in mind, however vague, and you can’t create a control mechanism that doesn’t lead to something that might otherwise be unlikely, i.e. a goal. This means that we could turn around the definition to get another one perfectly equivalent to the previous:
Definition 1B
A control mechanism is a feedback mechanism designed by humans;
→ a goal is the particular state, out of many possible, that the system tends toward as the result of that mechanism.
Usually we think of the goals first, and then seek control mechanisms that can achieve them. But nothing prevents you from starting with control first, and then seeing what “goal” it leads to.
For example, a chef trying to invent a new recipe does this when she puts ingredients together without fully understanding what the result might be. You do it, too, when you post a question on social media, awaiting reactions. These acts trigger “unconscious” feedback processes, their “goals” still to be revealed.
Perhaps, though, we would do better to use different words for these things, other than control and goals. We’ve seen that a control mechanism is just a special case of a feedback loop: an artificial one. “Goal”, then, is a term that only makes sense for human-planned things. The distinction is crucial.
What do we call the result of generic feedback loops, including those that were not designed, like the smooth pebble and the layered star?
Unfortunately I haven’t found a clear name for that in the scientific or philosophical literature. As far as I know, we don’t yet have a convenient word to discuss and reason about those “highly improbable outcomes made probable by recursion”.
But we need a word for this concept, as it’s essential for understanding and reasoning about reality. As a tribute to the beauty that such phenomena can produce, I propose the term Water Lily.
Definition 2
A Water Lily is the particular state, out of many possible, that a system tends toward as the result of a feedback loop.

A Water Lily is any outcome of feedback. It’s the “consistent behavior pattern over a long period of time” mentioned in Meadows’ quote. It’s what makes some parts of the Universal Network somewhat discernible from all the chaotic mess that surrounds it. It can take a variety of (improbable) forms: stable material shapes and arrangements, oscillatory motion, sudden explosions, total annihilation.
All goals set by people—the thermostat’s temperature setting, the goal of grabbing a ball in mid-air, your new year resolutions—they all involve trial and error, the feeding back of an outcome to inform the next action, and as such they are all Water Lilies. But not all Water Lilies are goals.
A flower blooming is a Water Lily because a web of feedback loops inside and across the plant’s boundaries blindly amplifies or stabilize certain behaviors until the flower happens. A growing baby is a Water Lily. The act of standing, the smooth pebble, the Lego outputs of a washing machine, and the tidy star are Water Lilies. Indeed, every solid object is a Water Lily because atomic bonds make feedback loops that prevent the atoms from going too near or too far from each other.
Once you start seeing things through this lens, most of the things to which we give names turn out to be Water Lilies. Many of them, like “solid objects”, are so commonplace that we take them for granted, as if they were metaphysical necessities. We forget that they, too, emerged from a chaotic mixture of particles interacting wildly with everything around them.
As for the less common Water Lilies, like the complex structure of an eye, we can’t help talking about them as if they had a purpose, e.g. “the eye evolved to see the optical wavelengths of light”. That’s not true. Rather, the eye evolved because there were feedback mechanisms involving light.
Goal-oriented expressions like that are harmless in most cases, and sometimes even helpful as simplified models, but they’re still false and often misleading, because goals and purposes always imply intelligent, planned action. Any non-random phenomena outside of intelligent, planned action can’t be said to be goal-oriented: they simply emerge as Water-Lilies, the products of feedback mechanisms.
The Universe we know, the collection of all things we’re ever capable of talking about, is made of Water Lilies. Recursion gives structure to it all, and allows for differences to arise at many scales. It’s how dynamical, complex behavior can arise and evolve into ever-more-unlikely outcomes.
Feedback doesn’t fully detach parts of the Universal Network from the rest, and for that reason it can’t give us neat, permanent boundaries—boundaries are still mostly in the eye of the beholder. Look closely enough, and you’ll always find that things are not so distinct as we make them out to be. But feedback gives us something to work with, some order and structure capable of supporting more order and structure, and that’s far better than nothing.
There is a missing piece in this line of reasoning, though. I wrote that, most of the time, thinking of Water Lilies as preceding their respective feedback mechanisms is thinking about things backwards. Why is it, then, that we always tend to think that way? That’s the topic of the third essay in this series. 💠
📬 Subscribe here to the Plankton Valhalla newsletter
Notes
- Cover picture: detail of Nénuphar 2, by Maurice Pillard Verneuil.
- Edit (June 19, 2025): I’ve corrected a mistake in the last paragraph.
- Edit (October 10, 2025): Renumbered the definitions for clarity.
- Edit (December 19, 2025): Updated to reflect that this is now a four-part series.
