Plankton 🥦 Valhalla

When two pieces of wood are rubbed together, they make fire.
When metal and fire are pushed together, the metal becomes molten.
Round things always spin.
Hollow things excel at floating.
This is their natural propensity.

We all need anchors and ropes. We’re afloat in an ocean of uncertainty and doubts. That ocean is here to stay, but we can learn to navigate it. My proposal, as in several of the other essays on Plankton Valhalla, is to equip ourselves with general and snappy tools for thinking. The more tools we have, the more powerful tools we can craft with them. Using what we already have, in what follows I want to introduce four (!) more tools that will serve us well when the waves are high and squalls sag the sails.

In The Invention of Systems, I started with the observation that Boundaries Are in the Eyes of the Beholder (BAEB): where one “object” ends and another begins is a matter of human choice, not a property of the world around us. We’ve been making this choice implicitly every time we’ve given a name to something. But, I argued in that essay, defining “systems” is often more useful:

While objects are about themselves and nothing else, systems are about what happens inside and outside of them, and are explicit about the fact that their boundaries are not set in stone.

Then, in Toying with Ideas of Glass Circuits, I used this diagram to talk about a generic system:

That’s pretty much as basic as it can get. It’s easy to grok. From here, I want to enrich this idea a little, turn it into something more functional that opens our way to more understanding of everything around us.

The premise to all that follows is that stuff, to take place, needs interactions. Only when two or more systems interact can anything happen—be it by the force of gravity, a transfer of sound waves or photons, the impact of a slap on a cheek. Exactly what it is that happens depends on three things:

1. the structure of the systems involved (how their matter is distributed),
2. their behaviors (how they’re changing and what comes out of them), and
3. their alignment.

Regardless of the details, every system is a physical arrangement of matter and energy. The way this matter is arranged is what we call the structure of the system, and it determines what happens when differences pass through the system.

Change the structure, and different things will happen. Move things around the human body even a little bit—say, move a fingernail to the inside of the heart—and chances are the body will stop working as it did before. A teacup’s structure is what allows it to be used to drink tea. A tectonic plate’s structure makes it more or less susceptible to earthquakes and drift. There is nothing happening in our reality, at any level of scale or complexity, that is not dependent on the structure of a suitably defined system.

Next, the flip side of structure: behavior. Things are almost never still: behavior is all that changes within and around the system. That includes the “Other stuff goes out” arrow in the diagram above, but also the changes in structure that go on inside the system without escaping its boundaries. Bowel movements, rocks rolling down a hill, civil wars, and all other events are the behavior of some system.

The relationship between structure and behavior is not always as plain as it sounds. What about, for example, a “computer system”? Part of its behavior is not too surprising, like displaying meaningful text and images on a screen. Even without understanding all the details, we can guess that it’s due to the shapes, materials, and other structural properties of the monitor, the cables, and other hardware components. Where it gets less obvious, though, is when you think about the programs running on the computer.

Does software have a physical structure too? Of course. Or rather, “software” is the name we give to the behavior of the hardware.

The solid state drives used in modern computers keep information in a gazillion floating-gate MOS transistors, all roughly sporting this same structure.

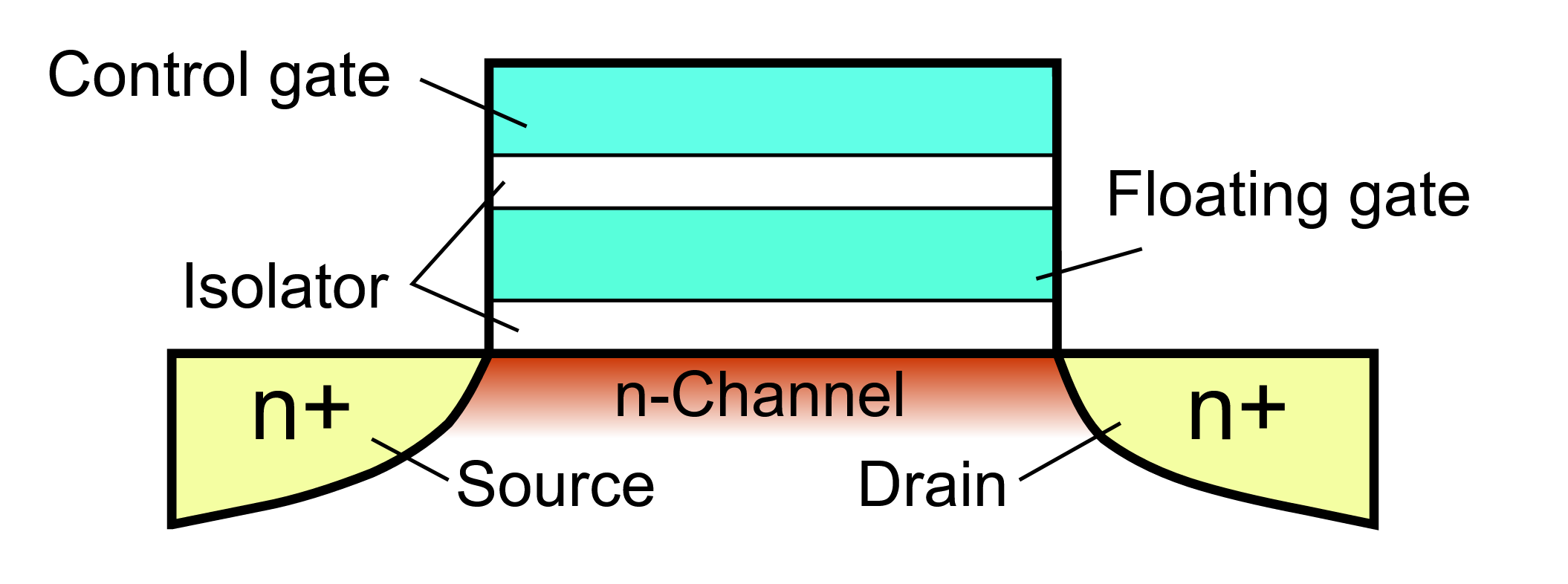
Information (the differences needed to remember and compute what the user wants) in the computer takes the structural form of the difference between the number of electrons and the number of protons in the chunk of silicon labeled “floating gate” in the picture. Of course, this is only a part of the structure that makes the machine do what it does.

And a “person system”? We have less clarity of the details here, but we know that information takes some kind of physical form, and that it’s probably the number of bulges (“dendritic spines”) on each neuron’s synapses. At the risk of oversimplifying a barely-understood theory: increase the number of spines on some synapses enough, and the person will start saying and doing different things than they would have said and done otherwise.

Of course, the structure of neurons is not all that matters for animal behavior. The rest of the nervous system, and most other organ systems of the human body, and even the environment are part of the structure that influences the final outcome.

Things get even more subtle and surprising when you try to control more complex systems like economies, governments, and ecosystems. Which is why we spend a lot of time figuring them out, creating whole disciplines such as anthropology, behavioral psychology, and economics. Probing those links is a fundamental task of humanity today.

Hunger, poverty, environmental degradation, economic instability, unemployment, chronic disease, drug addiction, and war, for example, persist in spite of the analytical ability and technical brilliance that have been directed toward eradicating them. No one deliberately creates those problems, no one wants them to persist, but they persist nonetheless. That is because they are intrinsically systems problems—undesirable behaviors characteristic of the system structures that produce them

This is very nice and all, but can we say anything more precise than “stuff takes place”? How do we think about behavior in practice? This is where our next two thinking tools come into play.

I use the word alignment here to mean how the interacting systems are positioned in space and time with respect to each other. Alignment is the distance, orientation, phasing, relative speed, and other geometrical and timing factors that determine whether a given interaction actually happens and how.

An aspirin pill won’t heal you if you put it in your ear ^{citation needed}. It only does its intended job when it’s “aligned” with your digestive system in a specific way (inside its hollow components, top-end entry).

Air at sea level has average temperatures in the life-enabling range of 273° to 293° Kelvin as long as the Sun and the Earth are “aligned” at a specific distance (which they fortunately are). Make the distance significantly shorter and the temperatures will shoot up. Make it longer, and the planet will freeze. Air temperatures also depend on a lot more things being aligned just right inside the atmosphere, like how many carbon atoms are in the air rather than underground.

As a thinking tool, alignment is useful when you try reasoning about emergence, synergy, and what systems do when they happen to have a “purpose”. More on that in later essays.

In practice, we talk about systems because we want to understand how their behavior affects whatever we care about. We crave to predict what the systems will do in the future, so that we may prepare for them, affect them, use them to our advantage.

If we knew with perfect exactitude the structure of the system, we might be able to predict a system’s behavior exactly. We would have no room for doubt. This is the hypothesis first proposed by a very smart folk who lived 200 years ago:

An intellect which at a certain moment would know all forces that set nature in motion, and all positions of all items of which nature is composed, if this intellect were also vast enough to submit these data to analysis, it would embrace in a single formula the movements of the greatest bodies of the universe and those of the tiniest atom; for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes.

Now, even if this idea, called “Laplace’s Demon”, were true—something which has been in doubt since we’ve discovered quantum mechanics—you and I are no demons.

For us puny mortals, ambiguity abounds in all directions. We never know things like the structures and alignment of two systems exactly enough to perfectly predict their behavior. Usually we know, based on the partial information we have, that there are a few possible outcomes, and we know that some of those outcomes are more probable than others, but we don’t know which one will actually become reality.

In other words, in our heads we have something resembling a sort of “tree” of potential outcomes that branches out into all possible behaviors of the interacting systems. We can’t tell for sure which of those possibilities—which branch of the future—will happen to come true, but we know that it’s probably one of them. I call this metaphorical branching out a tree of possibilities (ToP for short).

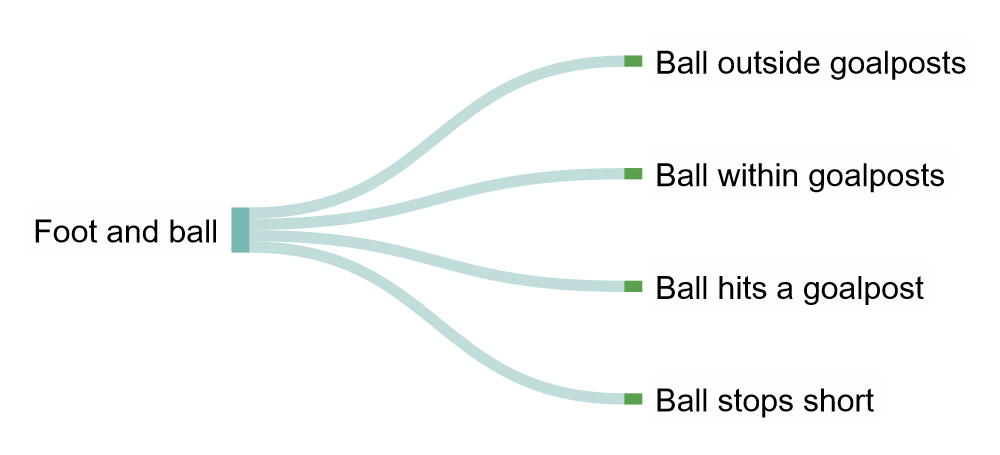
As an first example, consider a penalty shot in a soccer game.

On first approximation, this is an interaction between two systems: the soccer ball and the player’s foot. We know that there are a few possible outcomes, based on how the two will be aligned:

1. The ball can fly outside and beyond the goalposts (and crossbar).
2. The ball can end inside the goalposts (what the goalkeeper does isn’t important for this example.)
3. The ball can hit a goalpost or the crossbar.
4. The ball might stop rolling before even reaching the goal.

We can picture this as a “tree” with four branches:

But wait. We know something more about the composite system of ball + foot. From our experience watching or playing soccer games in the past, and from what we’ve heard from other people, we might remember that some of these branches are more probable—thicker—than the others.

For instance, it’s very rare for the ball to stop short of the goal, at least with professional kickers. We might also guess that it’s a bit rarer for the ball to hit a bar instead of going in or out of the goal’s rectangle, because the bars are relatively thin. But we may not be sure about which of the two other options is more likely. Updating our tree with this information, we get:

If you’re more familiar than me with this sport, you might object to the thicknesses of the above diagram. For example, you might say that it’s obviously more common for the ball to go within the goalposts (whether it is intercepted or not by the goalie). Also, if I told you that we’re talking about a specific player—say, Argentinian super-start Lionel Messi—you might be able to improve the tree even more, claiming that there’s no way his kick can stop short of the goal or fly past it!

And if I showed you a video of Messi running up to the ball and swinging his foot, but pausing the playback one millisecond before the kick actually happens, you might be able to improve your estimates of the tree’s branches by studying the leg’s swing.

All of this goes to highlight an important thing about trees of possibilities: the tree is a reflection of how much we know about the systems at play. I can’t stress that enough. The tree is not something that exists magically in the systems: it’s only in our heads. In fact, Laplace’s demon might crawl out of a hellish fracture in the ground to tell us that the tree should look like this:

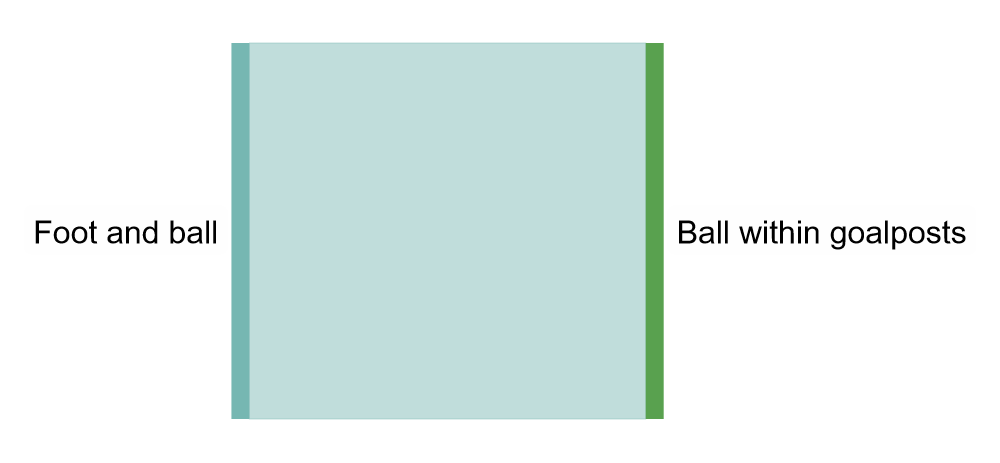
Only one branch, a 100% confidence that it will go within the goalposts (for example). The demon’s trees are all un-branching stumps.

If the demon does us the favor of telling us, we’d better listen, and bet all our money on that outcome. In all other cases, we’re stuck with our imperfect information, which gives us many-branched trees.

Of course, most of the imaginable outcomes have practically zero chances of happening. When the player kicks the ball, you can be pretty sure that it will not make the ball explode. When you clap your hands, you don’t expect to give birth to a swarm of butterflies.

Physical laws and ephemeral conditions constrain the shape of the tree: which branches exist, which combinations are allowed or prohibited, etc. We may be more or less familiar with these laws and conditions, but in most cases we have a range of possible outcomes in mind, and we can safely ignore the infinity of other imaginable effects.

For another example, let’s say you’re trying to bake a cake. When you put—you align—the dough in the oven, you might have this ToP in mind:

As you practice your baking skills over time, the “Delicious cake” branch will get fatter and fatter (as will your guests).

Very often we want to predict what will happen not after a single, specific interaction, but after two systems stay “more or less aligned” for “some amount of time”. This is especially common when one of the two systems is “the environment”, i.e. the part of the Universe around a given object/organism/system.

For instance, you might want to predict what happened to the wallet you dropped on a sidewalk thirty minutes ago. You could frame the situation like:

• System A = the wallet
• System B = the environment, i.e. the sidewalk and everything that existed near it in those thirty minutes

The ToP approach works just fine for such cases too, and as usual it reflects your knowledge of the systems. You’ll have to consider many more branches accounting for the broader range of outcomes that you can’t rule out in your uncertainty.

Here is how I would draw my ToP in the case of Tokyo, the city I live in:

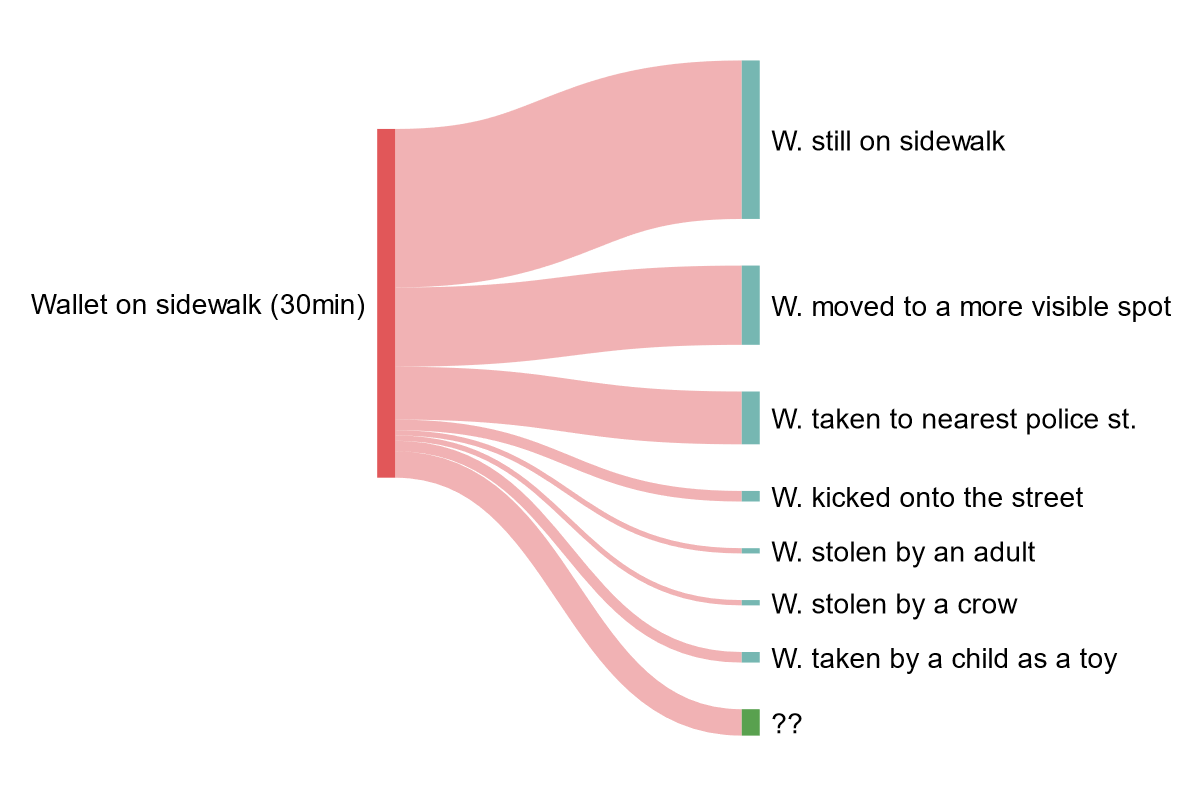
If you dropped the wallet in a shady corner of New York City instead, you might picture a fatter “stolen by an adult” branch than if you dropped it in central Tokyo. Each environment is different.

Note the “??” branch at the bottom, which I put there because my imagination and experience has limits. Maybe a hippo escapes from a zoo and eats the wallet, or the whole sidewalk is disintegrated by a terrorist’s bomb. We just don’t have all the knowledge necessary to determine all the branches of the tree in such high-uncertainty cases. Sometimes that’s fine, sometimes it isn’t, but that’s another story.

As far as thinking tools go, the structure, behavior, alignment and tree of possibilities of a system should feel natural to most people. I believe we do this kind of assessment about the world in our heads, all the time. In fact, you can find similar ideas in the work of thinkers from all ages and disciplines.

Ancient Chinese Taoist and Confucianist philosophers talked about the “propensities” of things, as in the quote at the beginning of this essay. A similar idea is discussed by modern philosophers, who call those propensities “dispositions”. “Structural determinism”, developed by biologists Humberto Maturana and Francisco Varela, strongly influenced my description of the link between structure and behavior. A concept of “possibility branches” is implicit in the idea of “affordances” in ecological psychology, and related to the mathematical construct of “configuration spaces”, so fruitfully employed by physicists. It’s also in the notion of Stuart Kauffman’s “adjacent possible”: the range of all possible futures that are one step away from the present. And it’s in this strangely energizing drawing by Tim Urban of Wait But Why:

It’s practically being rediscovered every five minutes!

Why, then, not use this idea more intentionally? Why not give it a memorable name, like “tree of possibilities”, and make it part of our sense-making toolkit? ■

📬 Subscribe to the Plankton Valhalla newsletter

Notes

• Cover image: The Turmoil of Conflict (Joan of Arc series: IV), Louis Maurice Boutet de Monvel, US National Gallery of Art.
• In the penalty kick example I listed a few simple branches of the tree of possibilities (“in”, “out”, “on a bar”, “stop short”). These won’t be enough if you’re goalkeeper: you need to split the “ball within goalposts” branch into finer twigs to be weighed, like “a little left of center”, “all the way to the top-right”, etc. This seems to be very tricky to estimate even for professionals.
• All the “tree diagrams” on this page are made with SankeyMATIC.
• For those confused about the word “alignment”: this has nothing to do with the field of “(AI) alignment” popular in the X-Risk community.
• More on dispositionalism and structural determinism.
• More on affordances.
• More on configuration spaces in math and physics.
• More on the Adjacent Possible.